TEA加密算法的实现与逆向分析

TEA算法

“TEA” 的全称为"Tiny Encryption Algorithm" 是1994年由英国剑桥大学的David j.wheeler发明的。

TEA算法也算是一种微型加密算法的。

在安全学领域，TEA（Tiny Encryption Algorithm）是一种分组加密算法，它的实现非常简单，通常只需要很精短的几行代码。

TEA算法使用64位的明文分组和128位的密钥，它使用Feistel分组加密框架，需要进行64轮迭代，但是作者认为32轮已经足够了，所以32轮迭代加密后最后得到的密文就是64位​。

简单的说就是，TEA加密解密是以原文以8字节（64位bit）为一组，密钥16字节（128位bit）为一组，（char为1字节，int为4字节，double为8字节），该算法加密轮次可变，作者建议为32轮，因为被加密的明文为64位，所以最终加密的结果也是64位。

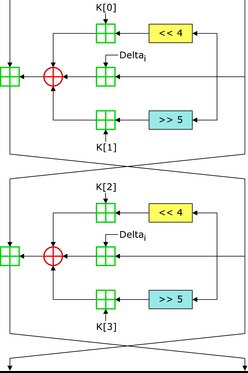
该算法使用了一个神秘常数δ作为倍数，它来源于黄金比率，以保证每一轮加密都不相同。但δ的精确值似乎并不重要，这里TEA把它定义为 ​​**δ=「(√5 - 1)231」​，这个δ对应的数指就是0×9E3779B9，所以这个值在TEA加密或者解密中会有用到。**

​

代码实现

#include <iostream>

//加密函数
void encrypt(uint32_t* v, uint32_t* k) {
    uint32_t v0 = v[0], v1 = v[1], sum = 0, i;              /* set up */
    uint32_t delta = 0x9e3779b9;                            /* a key schedule constant */
    uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];    /* cache key */
    for (i = 0; i < 32; i++) {                              /* basic cycle start */
        sum += delta;
        v0 += ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);
        v1 += ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);
    }                                                       /* end cycle */
    v[0] = v0; v[1] = v1;
}


//解密函数
void decrypt_tea(uint32_t* v, uint32_t* k) {
    uint32_t v0 = v[0], v1 = v[1], sum = 0xC6EF3720, i;     /* set up */
    uint32_t delta = 0x9e3779b9;                            /* a key schedule constant */
    uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];    /* cache key */
    for (i = 0; i < 32; i++) {                                  /* basic cycle start */
        v1 -= ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);
        v0 -= ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);
        sum -= delta;
    }                                                           /* end cycle */
    v[0] = v0; v[1] = v1;
}

使用示例：

int main()
{
    char data[] = "password123456789";
    uint32_t key[] = {0x11111111,0x22222222,0x33333333,0x44444444};

    for (size_t i = 0; i < strlen(data)/8; i++) encrypt((uint32_t*)&data[i*8], key);
    printf("加密后：%s\n", data);

    for (size_t i = 0; i < strlen(data)/8; i++) decrypt((uint32_t*)&data[i*8], key);
    printf("解密后：%s\n", data);

}

IDA伪代码

VS2022 64位 release编译，IDA打开：

加密部分：可以看到，delta值的形式变了

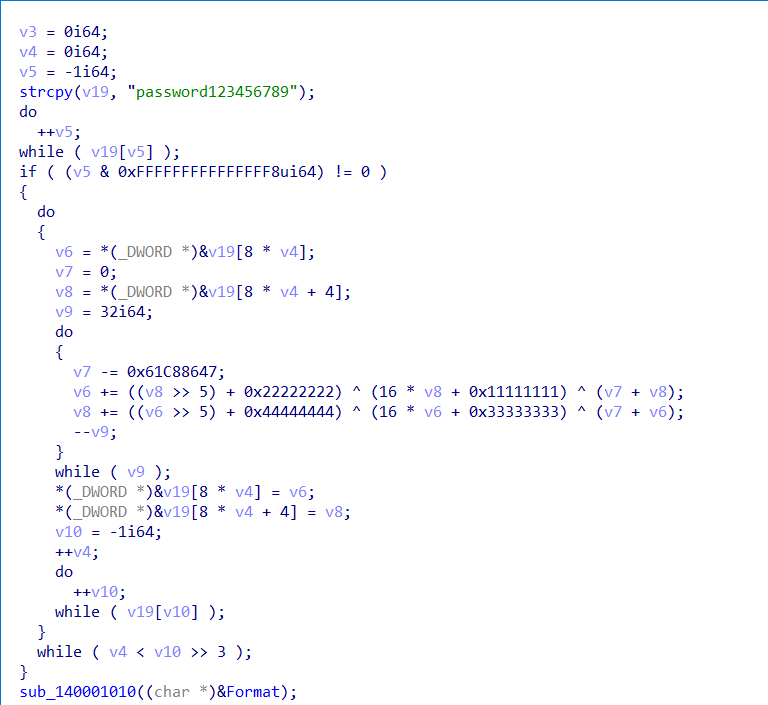
解密部分：

​

Tips

• TEA算法的特征是delta值和16字节的密钥（128位）以及32轮迭代

  • 这些东西可以魔改，如果没魔改过，插件可以识别出该算法，否则需要算法结构手动找

• x-=0x61c88647和x+=0x9e3779b9，这两个值是等价的

XTEA算法

TEA 算法被发现存在缺陷，作为回应，设计者提出了一个 TEA 的升级版本——XTEA。

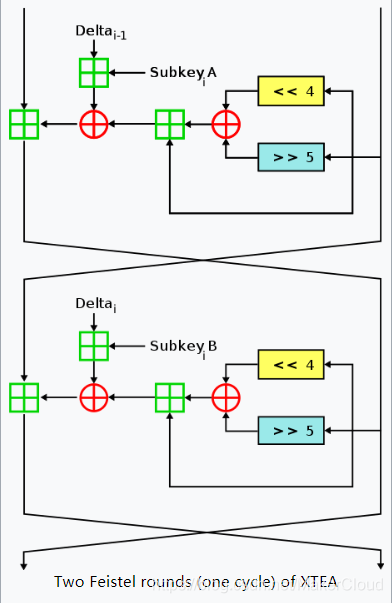
XTEA是TEA的扩展，也称做TEAN，它使用与TEA相同的简单运算，同样是一个64位块的Feistel密码，使用128位密钥，建议64轮，但四个子密钥采取不正规的方式进行混合以阻止密钥表攻击

​

代码实现

void encrypt_xtea(uint32_t num_rounds, uint32_t v[2], uint32_t const key[4]) {
	uint32_t i;
	uint32_t v0 = v[0], v1 = v[1], sum = 0, delta = 0x9E3779B9;
	for (i = 0; i < num_rounds; i++) {
		v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
		sum += delta;
		v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3]);
	}
	v[0] = v0; v[1] = v1;
}

void decrypt_xtea(uint32_t num_rounds, uint32_t v[2], uint32_t const key[4]) {
	uint32_t i;
	uint32_t v0 = v[0], v1 = v[1], delta = 0x9E3779B9, sum = delta * num_rounds;
	for (i = 0; i < num_rounds; i++) {
		v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum >> 11) & 3]);
		sum -= delta;
		v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
	}
	v[0] = v0; v[1] = v1;
}

使用示例：

int main()
{
    char data[] = "password12345678";
    uint32_t key[] = {0x11111111,0x22222222,0x33333333,0x44444444};

    for (size_t i = 0; i < strlen(data) / 8; i++) encrypt_xtea(32,(uint32_t*)&data[i * 8], key);
    printf("加密后：%s\n", data);

    for (size_t i = 0; i < strlen(data) / 8; i++) decrypt_xtea(32,(uint32_t*)&data[i * 8], key);
    printf("解密后：%s\n", data);
}

IDA伪代码

加密部分：这编译出来居然给把循环平坦铺开了…

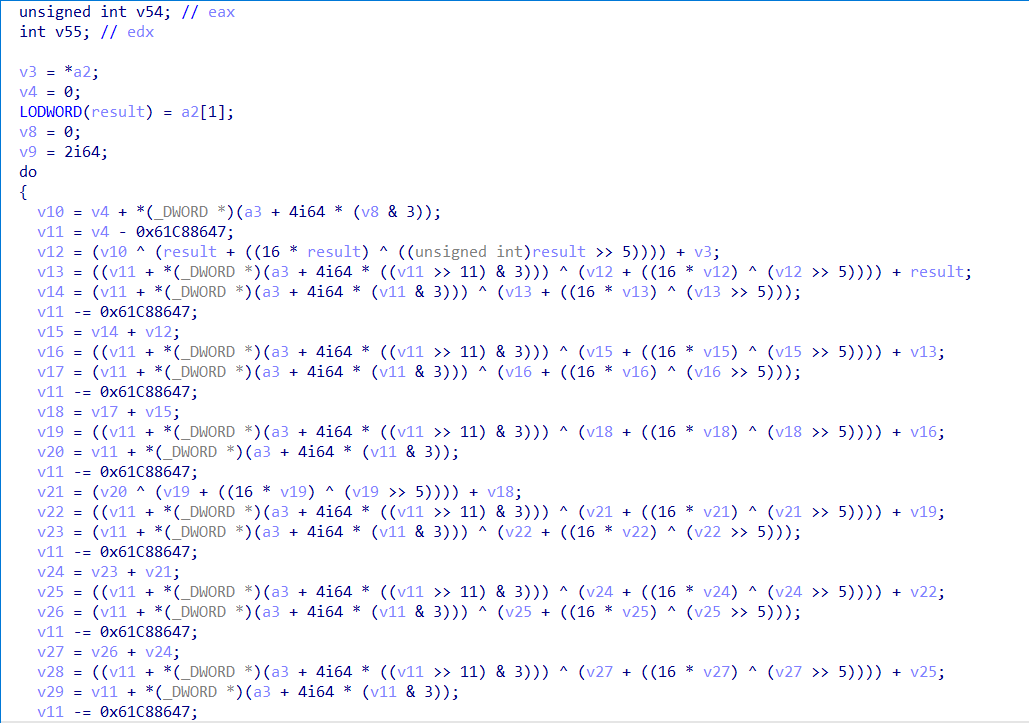
解密部分：依然是铺开了的循环

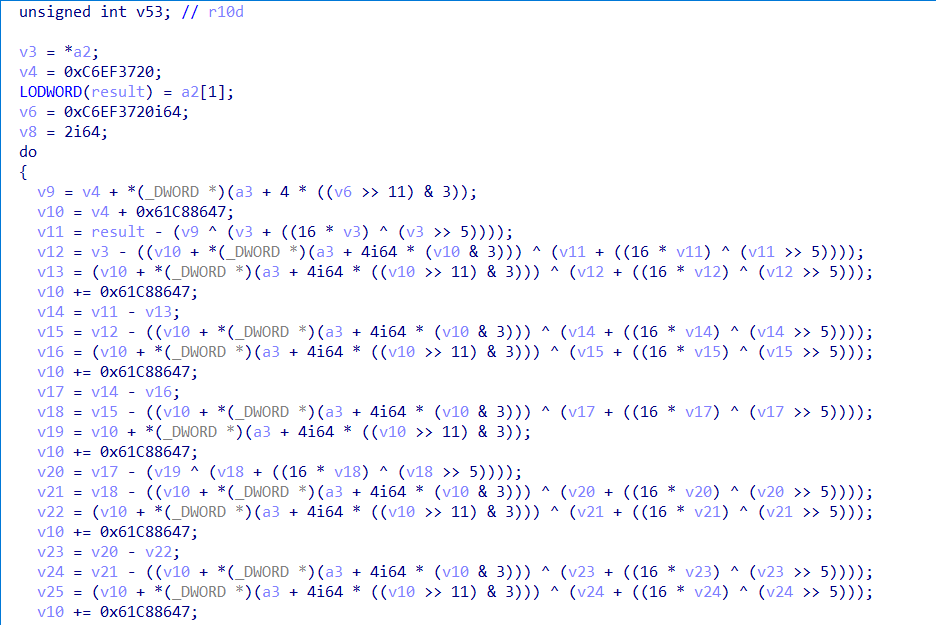
可以看到，和普通的TEA算法相比，差不多，但是异或的值出现了特征，就是这里计算的两个值，不管是加密还是解密，都出现了&3的操作，

Tips

• 最显眼的特征：原先TEA算法的v1 + sum​变成了(sum + key[sum & 3])​以及sum + key[(sum>>11) & 3]​
• 可以魔改的点依然是Delta的值，轮数

XXTEA算法

在经历了块加密的问题之后，XTEA再度进化， 变成了支持块加密XXTEA​。

XXTEA是一个非平衡Feistel网络分组密码，在可变长度块上运行，这些块是32位大小的任意倍数（最小64位），使用128位密钥, 是目前TEA系列中最安全的算法，但性能较上两种有所降低。

​

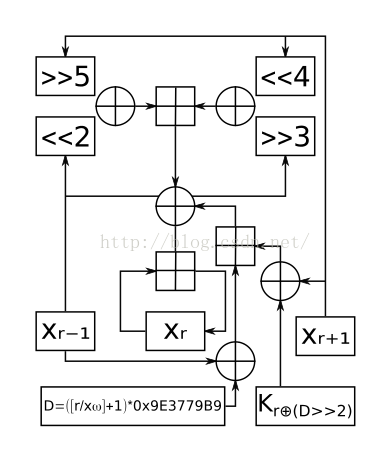
代码实现

#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z)))

void btea(uint32_t* v, int n, uint32_t const key[4])
{
    uint32_t y, z, sum;
    unsigned p, rounds, e;
    if (n > 1)            /* Coding Part */
    {
        rounds = 6 + 52 / n;
        sum = 0;
        z = v[n - 1];
        do
        {
            sum += DELTA;
            e = (sum >> 2) & 3;
            for (p = 0; p < n - 1; p++)
            {
                y = v[p + 1];
                z = v[p] += MX;
            }
            y = v[0];
            z = v[n - 1] += MX;
        } while (--rounds);
    }
    else if (n < -1)      /* Decoding Part */
    {
        n = -n;
        rounds = 6 + 52 / n;
        sum = rounds * DELTA;
        y = v[0];
        do
        {
            e = (sum >> 2) & 3;
            for (p = n - 1; p > 0; p--)
            {
                z = v[p - 1];
                y = v[p] -= MX;
            }
            z = v[n - 1];
            y = v[0] -= MX;
            sum -= DELTA;
        } while (--rounds);
    }
}

使用示例：

int main()
{
    char data[] = "password12345678";
    uint32_t key[] = { 0x11111111,0x22222222,0x33333333,0x44444444 };

    int n = strlen(data)/8;
    // n的绝对值表示v的长度，取正表示加密，取负表示解密
    // v为要加密的数据是两个32位无符号整数
    // k为加密解密密钥，为4个32位无符号整数，即密钥长度为128位

    for (size_t i = 0; i < strlen(data) / 8; i++) btea((uint32_t*)&data[i*8], n, key);
    printf("加密后：%s\n", data);

    for (size_t i = 0; i < strlen(data) / 8; i++) btea((uint32_t*)&data[i*8], -n, key);
    printf("解密后：%s\n", data);
}

IDA伪代码

加密部分：

​

解密部分：

​

Tips

XXTEA算法的解密同样只是对加密算法的数据处理顺序进行倒置，同时加法改减法（减法改加法）

逆向处理思路

这类算法比较常见于逆向中，在分析二进制文件中的算法的时候有几个识别的特征:

• 可能存在针对64bit以及128bit数字的操作（输入的msg和key）
• 存在先进行位移，然后异或的类似操作（(z>>5^y<<2)​这类混合变换）
• 前面一个复杂的混合变换的结果可能会叠加到另一个值上，两者相互叠加（Feistel 结构）
• 获取密钥的时候，会使用某一个常量值作为下标（key[(sum>>11) & 3]​）
• 会在算法开始定义一个delta，并且这个值不断的参与算法，但是​从来不会受到输入的影响​（delta数值，根据见过的题目中很少会直接使用0x9e3779b9）

解决逆向题大部分出现TEA的场合都是【识别算法->编写对应解密程序】，将上述的算法进行逆推即可得到解密。

参考资料

• [1] 逆向分析中的密码学—tea_努力学习的大康的博客-CSDN博客
• [2] tea系列算法速成总结及其在PWN中运用 - 知乎 (zhihu.com)
• [3] TEA/XTEA/XXTEA系列算法 - zpchcbd - 博客园 (cnblogs.com)
• [4] TEA加密 - Sk2rw - 博客园 (cnblogs.com)
• [5] TEA系列算法101-安全客 - 安全资讯平台 (anquanke.com)

‍